Michel Vinais : Résolution... Problème mathématique

S'engager dans la résolution de problèmes revient à entamer une odyssée impliquant l'individu dans la globalité de son fonctionnment psychologique et mental. (Cf H.Planchon)

S'affronter à un problème n'est pas une expérience indifférente, tant pour l'élève en classe de mathématiques que pour l'adulte régulièrement aux prises avec un ensemble de réalités hétérogènes, donc potentiellement contradictoires et conflictuelles.
Un problème naît de la confrontation avec une impossibilité, une discontinuité voire un paradoxe dont l'évidence nous fait violence. A cet égard, le problème mathématique présente une exemplarité qui empêche de ne voir en lui qu'exercice futile aux enjeux exclusivement scolaires. C'est qu'il éveille des émotions, suscite des réactions, sollicite des comportements symptomatiques à maints égards de notre façon d'appréhender le réel, en tous cas formellement analogues à ce qui se trouve mis en jeu dans les rapports complexes que chacun entretient constamment avec soi-même comme avec le monde extérieur.
Un problème, ce n'est pas le choc des cultures mais le choc des structures : une structure de départ (la situation problème, l'énoncé) qui nous est donnée et une structure finale (la solution) englobant la première et qui est soit à inventer soit à retrouver. Entre les deux : le vide, plus exactement le manque-à-lier que met à jour l'occultation énigmatique des relations qui permettraient de passer de l'une à l'autre. En ce sens, le problème c'est l'appréhension d'une distance apparemment irréductible séparant deux organisations distinctes (l'une réelle, l'autre virtuelle). Traiter le problème revient alors à réunir les deux pôles en élaborant un système original susceptible de prendre en compte, d'articuler et d'intégrer à la fois la situation de départ et l'objectif. La nouvelle unité ainsi créée, en tissant des liens vient cicatriser l'effraction occasionnée par la question et par là apaiser une tension, oblitérer une lacune, restaurer un équilibre.

D'un point de vue technique, la résolution du problème passe par la mise en œuvre d'un certain nombre d'outils relevant en fait de l'exploitation de problèmes antérieurement résolus. Entendons par là :
* d'une part, les théorèmes, propriétés, définitions, lois, concepts et techniques assimilés par l'apprenant comme appartenant à sa - à la culture mathématique et dont il pourra user directement, c'est-à-dire sans avoir à refaire le chemin parcouru par ceux qui se sont affrontés au problème - au sens propre du terme - d'établir de tels instruments notionnels ;
* d'autre part, les problèmes mathématiques déjà connus de l'apprenant et dont la fréquentation a nourri l'expérience qu'il a de ce type d'exercices.

Une certaine familiarité tant avec les objets mathématiques et leurs " mœurs " qu'avec les problèmes mathématiques et leur " folklore " constitue en effet un contexte favorable au déploiement des processus de résolution comme à leur aboutissement. C'est au cours, au décours souvent, d'une activité tour à tour dispersive et intégrative faite de rumination, de manipulations, de mises en relation des données, puis des notions évoquées par les données, puis des notions évoquées par les notions, que surgit la révélation du chaînon manquant susceptible de faire le lien entre ce que l'on a et ce vers quoi l'on tend. Une telle découverte, en levant le voile, donne alors prise à l'élaboration de la solution, laquelle viendra saturer/suturer un énoncé en souffrance et momentanément combler/colmater un sujet en mal de complétude. De même, c'est par association d'idées et recherche d'analogies que le problème du moment pourra être rapproché d'une ou plusieurs situations déjà rencontrées, qu'une structure (ou partie de structure) sera reconnue au sein du questionnement actuel, faisant d'elle la clef à même de faire jouer/jouir une serrure qui ne demandait qu'à céder pour rétablir la communication entre deux nombres orphelins.
Encore faut-il pour cela que l'individu ait réussi à s'engager effectivement et pleinement dans un processus de recherche ; ce qui n'a rien d'évident ; qu'on en juge :
Pour traiter un problème, en effet, il faut pouvoir (et l'énumération n'est pas exhaustive) se prendre au jeu d'une recherche gratuite par certains côtés, supporter des émotions souvent intenses, s'activer à imaginer des hypothèses, à bâtir des stratégies, à alimenter un questionnement permanent, s'arracher à la paralysie qui tend à envahir l'esprit, se hasarder dans l'inconnu sans savoir si l'on va trouver, tolérer un certain désordre intérieur, se plier à vérifier et critiquer les cheminements dans lesquels on s'est engagé, s'exposer à l'erreur et à l'échec. Autant dire qu'à la violence et à l'insistance du problème doivent répondre l'audace et la ténacité de celui que entreprend de s'y colleter.

On peut alors tout à fait comprendre qu'il soit plus confortable et surtout plus économique à certains de court-circuiter purement et simplement le temps de la recherche - temps de la mobilisation et de l'incertitude intellectuelles. En ce cas, on voit l'apprenant attendre que la solution lui soit donnée, estimant -à tort- que comprendre le corrigé revient à savoir faire le problème - alors que, faute d'avoir été réellement vécue, l'expérience du problème restera lettre morte et sera difficilement réutilisable ultérieurement. La conception - l'illusion - sous-jacente à une telle attitude est que la solution pourrait être trouvée sans avoir à être cherchée ; elle est censée illuminer par la grâce d'une imposition sinon surnaturelle du moins méta-intellectuelle.
Cependant, ce type de raisonnement, défensivement dressé contre ce que toute investigation a d'inquiétant, de douloureux et de difficile, résiste mal à l'insistante et lancinante sollicitation exercée par le problème. Aussi certains n'ont-ils d'autres recours pour soulager la tension que le " passage à l'acte " qui va consister à plaquer sur l'énoncé la première structure venue sans que sa pertinence soit soumise à vérification. Sa fonction se réduisant à colmater une lacune (extérieure à l'individu mais ressentie avec l'acuité propre à ce qui fait écho à l'intérieur de soi) autant qu'à évacuer l'appel au travail sur le sens.
De telles stratégies, plus ou moins consciente, ont leur logique propre, qui est celle de l'exonération et de l'apaisement à court terme. L'évitement actif et le placage hâtif viennent en place d'une confrontation, certes formatrices mais dont la pénibilité le dispute à l'aléatoire.
Notons cependant que l'effort de construction n'intervient pas seulement en amont de la découverte mais également en aval.

En effet, une fois la solution trouvée il faut encore s'astreindre à la valider : pour soi avec la recherche de preuves, pour autrui au moyen d'une mise en mots susceptible d'exposer de façon convaincante le raisonnement jugé le plus direct et le plus élégant à relier l'énoncé à la solution ; cela en un cheminement conforme au rituel comme aux canons (à la fois esthétiques et logiques) propres à toute démonstration mathématique. Il s'agit de témoigner " urbi et orbi " que l'on a triomphé du Sphinx, que l'on s'est véritablement rendu maître du problème.
Naturellement une telle communication idéalement linéaire, fluide, harmonieuse, policée, sans faille ni ambiguïté, sans contradiction ni solution de continuité, contraste fortement avec le désordre chaotique dans lequel a baigné l'investigation qui l'a précédé - désordre auquel pourtant elle doit tout.
Le propos de la solution écrite est de rendre objectif ce qui était intuitif, partageable ce qui était personnel, linéaire ce qui était global, net ce qui était brut ; d'où la nécessité de gommer ce qu'elle doit au bricolage laborieux traversé d'errances et criblé d'erreurs par lequel il a fallu passer avant de pouvoir présenter un produit fini et poli dont la perfection affichée sera à même de contenter certaines des figures mythologiques qui peuplent notre monde intérieur, et d'en réparer ou dédommager certaines autres.
On le voit, s'engager dans la résolution de problèmes revient à entamer une odyssée impliquant l'individu dans la globalité de son fonctionnement psychologique et mental.

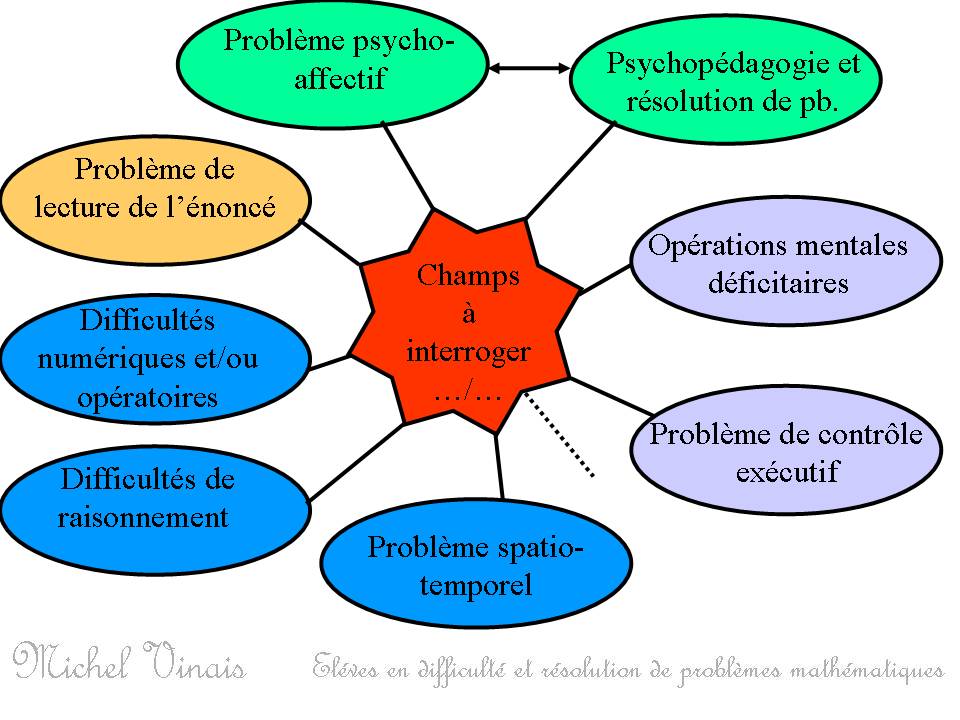
Ce discours nous permet d'appréhender quelque peu la complexité de la situation mais amener des élèves en difficultés (Projet d'aide spécialisée à dominante pédagogique, CAPA SH option E) voire en grandes difficultés (Perturbations psychiques et/ou troubles importants des fonctions cognitives, CAPA SH option D) à se "colleter" à ces situations, à "s'engager pleinement et effectivement", à "entamer une odyssée impliquant l'individu dans la globalité de son fonctionnement psychologique et mental" nous invite à interroger différents champs interpellés lors de la confrontation à de telles situations afin de comprendre ce qui se passe. Et c'est bien la compréhension de la situation, la compréhension du sujet dans cette situation, ce à quoi il se heurte, ce à quoi l'enseignant se heurte, qui devraient permettre de mieux intervenir.

Le schéma suivant formalise différents champs en jeu dans la résolution de problème, champs que l'enseignant spécialisé se doit d'interroger pour analyser et comprendre la situation à laquelle se trouve confronter les élèves qui lui sont confiés afin d'intervenir de manière cohérente en prenant en compte à la fois la problématique du sujet et ce que provoque, ce que convoque la situation.

Formalisation du discours sur ce schéma à venir. En attendant, ci dessous diaporama, appui de cours.

Résolution...problème mathématique